对轴向柱塞泵出口压力信号进行采集,对柱塞泵正常运转和单柱塞脱靴故障状态的泵出口压力信号进行关联维数计算分析。
1、实验条件
在轴向柱塞泵的诸多失效形式中,脱靴故障是其主要故障形式之一。本文对某台液压
数控折弯机液压伺服系统中的液压泵进行状态监测与故障诊断,液压折弯机的整体如图6.5所示。采用破坏性实验,将斜轴式柱塞泵的七柱塞中的一个脱靴处理。利用压力传感器对轴向柱塞泵出口压力进行监测。传感器输出信号经虚拟仪器NI.DAQ卡进行采集,并送计算机进行分析处理。本系统的数据采集与处理采用了赢拟仪器平台软件LabVIEW。
实验数据是用液压泵在正常工作和发生单柱塞脱靴故障时,采集到的液压泵出口压力脉动数据。电动机工作转速为l500r/rain,采样频率选为10kHz。轴向柱塞泵型号及参数为:MCYl4.B,7柱塞,理论排量10ml/r,公称压力25MPa,驱动电动机Y132M。4,额定转速1 500r/min。系统压力调定为3MPa。
图6分别为液压泵在正常工作状态和脱靴故障状态下的时域曲线。由图中可以看出,故障状态下的压力信号脉动周期明显大于正常压力信号的脉动周期。下面从关联维数的角度较两者信号有何不同,计算关联维数之前首先要进行信号的小波消噪预处理。

图5数控折弯机
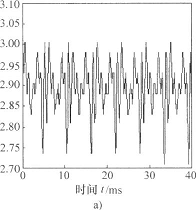
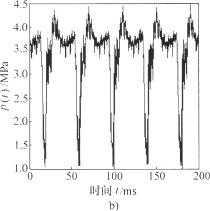
图6泵出口压力信号 a)正常压力信号b)故障压力信号
2、信号的小波消噪与特征提取
泵压力信号的信噪比低、冲击信号丰富,具有非平稳性。需要对其进行小渡清噪处理,减少噪声的影响,提取
液压折弯机故障特征频率
为了分析信号的运行频率特征,下面对消噪后的信号进行分解。图7为正常压力信号的小波分解,小波系数单位均为MPaosl为消噪后的信号,分解层次囊10层,分解的小波函数采样Daubechies 5级小波。
生理采用了虚重数的角度比页处理。

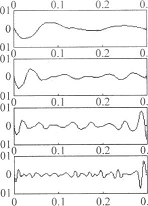
正常压力信号的小波分解
由于该系统柱塞泵的柱塞数为7,转轴频率为理论流量脉动频率为转轴频率的14倍,即为由小波分解可以看到,在d8频段,显示的是泵的基频,在d4频段,显示的是泵的流量脉动。经过去噪后的正常压力信号的脉动频率与理论流量脉动频率相同。
为了对故障信号的突变点进行定位,并提取故障特征频率,下面对故障信号消噪后的信号 进行分解,分解层次为10层,分解的小波函数仍采样5级小波。图8为液压折弯机故障信号的分解结果,小波系数单位均为MPa。由于单柱塞脱靴的影响,泵每转一周,有一次压力突降,造成泵每转一周有一次冲击振动,即单柱塞脱靴故障特征信号为d8中提取了故障特征频率而d4中提取了系统运行信息即流量脉动频率实验结果与理论分析一致。
3、关联维数计算
为了得到液压
折弯机液压泵正常工作状态和发生脱靴故障后信号变化的定量化信息,应用.算法,分别计算两种状态下信号的关联维数数值。
对于延时丁的选取,由于基于自相关函数的方法比较简单,易于计算,并能合理地提供由冗余到不相关的比较折中的度量,故仍采用自相关函数法取得延时下的数值。取经过小波去噪后的长度为3的信号,应用软件编制程序,绘制延时下与自相关函数R(丁)关系曲线,取自相关函数第一次为零时的r值作为延时值。图6.为压力下的泵正常和故障状态下压力信号的自相关函数曲线。通过改变图形显示坐标范围,可以得到正常状态和故障状态的自相关函数第一过零点延迟时间分别为0.7ms和6.1ms。
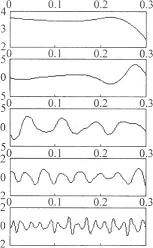
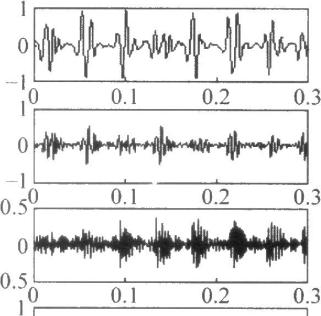
图8液压折弯机故障压力信号的小波分解
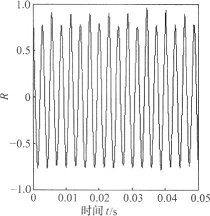
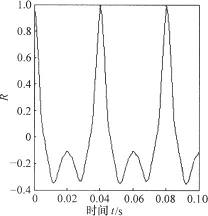
图9压力信号自相关函数 a)正常压力信号b)故障压力信号
编写MATLAB程序,通过不断增大嵌入维数,得到收敛的关联维数。在饱和嵌入维数为15时,得到3MPa压力下,液压泵正常工作状态压力信号的关联积分和局部斜率曲线如图10所示。同样,3MPa压力下,饱和嵌入维数为14时故障状态压力信号的关联积分和局部斜率曲线如图11所示。
对液压折弯机正常状态和故障状态的局部斜率曲线中平滑的部分进行最dx--乘法拟合直线数。在饱和的关联积分》14时故障
法拟合直线斜率,得到相应的关联维数。
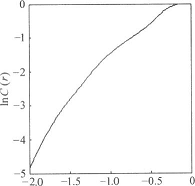
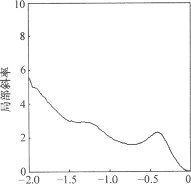
图10正常状态下关联积分及局部斜率
图11 故障状态下关联积分及局部斜率
a)关联积分b)局部斜率 a)关联积分b)局部斜率
表2为液压泵正常工作和发生脱靴故障时在不同嵌入维数时关联维数的计算结果。
表2嵌入维数及关联维数值
嵌入维数 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
正常关联维数 | 1.42 | 1.57 | 1.61 | 1.65 | 1.68 | 1.67 | 1.66 | 1.68 | 1.67 | 1.66 |
故障关联维数 | 1.07 | 1.23 | 1.32 | 1.35 | 1.34 | 1.35 | 1.34 | 1.35 | 1.33 | 1.35 |
由表2可以看出正常和故障状态下的饱和嵌入维数分别为15和14。表6-3为液压泵正常工作状态和发生脱靴故障状态下的关联维数计算值及其重构参数。
表3重构参数及维数值
状态 | 饱和嵌入维数 | 延迟时间/ms | 数据长度Ⅳ | 饱和关联维数D2 |
正常 | 15 | 0.7 | 3 000 | 1.68 |
故障 | 14 | 6.1 | 3 000 | 1.35 |
4、结果分析
由表3可以看出,液压折弯机故障工作状态下的压力信号的关联维数小于正常状态的关联维数。当柱塞泵发生脱靴故障时,由于单柱塞脱靴的影响,泵每转一周,有一次压力突降,造成泵每转一周有一次冲击振动。压力脉动信号将在相空间趋于某一有限维吸引子,计算得到的关联维数将小于正常状态下的关联维数。分维数计算结果与实验结果分析相一致。
液压泵在不同工作状态下有明显不同的关联维数,通过利用压力信号的关联维数可以有效地监测液压泵的工作状态,诊断故障的发生。将混沌及分形理论用于监测液压折弯机设备的工作状态,这方面的深入研究可以为液压设备的工作状态监测拓展思路,有助于提高监测的质量。
表3 F=0.729时两种算法得到Lyapunov指数
算法 | A1 | A2 | 计算时间/s | 分维数 | 误差 |
标准QR算法 | 0.08 3.473 | -0.364954 | 437 | 2.281 | 6.173e-2 |
改进QR法 | 0.135963 | -0.435958 | 284 | 2,342 | 1.667e-5 |
表4 F=0.760时两种算法得到Lyapunov指数
算法 | A1 | A2 | 计算时间/s | 误差 |
标准QR算法 | -0.143209 | -0.146783 | 579 | 3.336e-2 |
改进QR算法 | -0.127387 | -0.172603 | 212 | 3.333e-5 |
图9和图10所示的Lyapunov指数时间演化曲线表明,两种算法都有较好的收敛性,但是从表3和表4看出,QR算法的计算时间比改进的QR算法时间要长得多,而且误差也要比改进算法大。这说明改进的QR算法要比标准的QR算法优越。










